Reibungsberechnung auf energetischer Grundlage

Die gesamte Reibungsenergie setzt sich aus den in der folgenden Abbildung dargestellten Energieanteilen zusammen. Sie können die jeweiligen Reibungsenergieanteile anklicken. Damit gelangen Sie direkt zu den entsprechenden Erläuterungen.

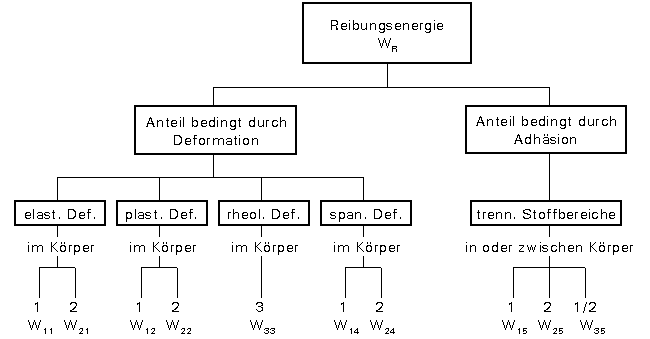
Die gesamte Reibungsenergie teilt sich in verschiedene Energieanteile auf. Die Quantifizierung stellt ein wichtiges Problem bei der Berechnung von Reibung und Verschleiß dar. Die Unterteilung in Deformations- und Adhäsionsanteil wird auch als Doppelnatur der Reibung bezeichnet. Die Reibungsenergie, wie sie im folgenden betrachtet wird, setzt sich aus der Summe der Energieanteile zusammen und ist demnach

(5.1)

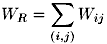
Betrachtet man einen Energieanteil für sich, so berechnet sich dieser als das Produkt aus der Energiedichte eines Mikrokontaktes, der Anzahl am Reibungsprozeß beteiligter Mikroerhebungen gleichartiger Energiearten sowie dem beanspruchten Volumen:

(5.3)

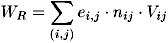
Die mittlere Reibungsschubspannung kann dann berechnet werden, da der Reibweg bekannt ist und die Fläche bereits in der Kontaktgeometrie bestimmt wurde. Es ist

(5.6)

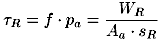
Etwas umgeformt erhält man dann mit Hilfe den allgemeinen Beziehungen für die Reibungszahl (Gleichung 3.1) und die Reibungsenergie (Gleichung 3.3) eine Beziehung zur Ermittlung der Reibungszahl:

(5.7)

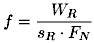
Der Deformationsanteil der Reibungsenergie setzt sich wiederum aus unterschiedlichen Anteilen zusammen: der elastischen, der plastischen, der rheologischen und der spanenden Deformation. Eine kurze Erläuterung und die zugehörigen Bestimmungsgleichungen sind in den folgenden Abschnitten aufgeführt.

Bei der reinen elastischen Deformation verformen sich die Mikroerhebungen bei realem Kontakt. Bei anschließender Entlastung, nimmt die Mikroerhebung ihre vorherige Gestalt exakt wieder an. Es treten keine bleibenden Veränderungen auf.

Für diese Deformationsart errechnet sich die Energiedichte näherungsweise aus den Kennwerten aus dem Spannungs-Dehnungs-Diagramm des einachsigen Zugversuchs

(5.9)

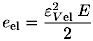
(5.10)

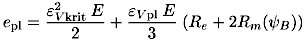
Eine bessere Möglichkeit für die Erfassung der plastischen Deformation bieten Formänderungsschaubilder von Umformprozessen. Da sie aber momentan nicht für die gebräuchlichen Reibungswerkstoffe vorliegen, wird auf die oben genannten Näherungsgleichungen zurückgegriffen.

Zusätzlich zu den für die Festkörper ermittelten Energiedichten muß bei geschmierten Reibpaarungen die Energiedichte für den Schmierstoff berücksichtigt werden. Dazu stehen zwei alternativ zu verwendende Formeln zur Verfügung. Nach Hadler [10] kann die rheologische Energiedichte berechnet werden nach

(5.14)

Kuhn [14] gibt folgende, ähnliche Gleichung an:

(5.15)

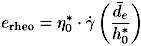
Die Energiedichte bei spanender Deformation (Mikroschneiden) kann mittels der spezifischen Schnittkraft nach Thomas [24] bestimmt werden als

(5.11)

Adhäsionsanteil der Reibungsenergie

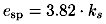
Die Berechnung der Energiedichte bein Lostrennen von Adhäsionsverbindungen kann auf zwei verschiedene Arten erfolgen. Eine Möglichkeit ist, die Trennung hauptsächlich als Scherung (im weicheren Reibkörper) aufzufassen. Die Berechnungsgleichung für diesen Fall lautet

(5.12)

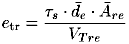
Alternativ kann auch mit der Sublimationsenergiedichte gerechnet werden [12, 25]. Dafür steht dann die folgende Gleichung zur Verfügung:

(5.13)

Gleichartige Energieanteile

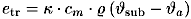
Zur Bestimmung der gleichartigen Energieanteile bei elastisch-plastischem Kontakt muß zwischen den beiden Kontaktmodellen unterschieden werden:

• Für den Kontakt rauh/glatt (Modell Kugel/Ebene) gilt: in beiden Reibkörpern liegen unterschiedliche Deformationsmechanismen vor. Es wird angenommen, daß der Reibkörper 1 der härtere der beiden ist. In diesem Fall tritt in diesem sowohl elastische, als auch plastische Deformation auf. Demnach ist die Summe der elastischen und plastischen Kontake (jeweils berechnet im Abschnitt 4) beim Reibkörper 1 gleich der Gesamtanzahl der Kontakte im zweiten Reibkörper, in welchem nur plastische Kontakte existieren.

• Für den Kontakt rauh/rauh (Modell Kugel/Kugel) gilt: in beiden Reibkörpern liegen identische Deformationsmechanismen vor. Daraus ergibt sich, daß in beiden Reibkörpern sowohl elastische, als auch plastische Kontakte vorkommen. Unter den für dieses Kontaktmodell getroffenen Einschränkungen (gleiche Kontaktanzahl, gleiche Werkstoffe, etc.) folgt daraus, daß die Anzahl der elastischen und plastischen Kontakte in beiden Reibkörpern gleich ist.

Ist die Härte der beiden Reibkörper sehr unterschiedlich wie z.B. bei der Paarung Metall/Mineral, so berechnet sich die Anzahl der Energieanteile aus der Anzahl der plastischen Kontaktstellen des weicheren Reibkörpers.

Für die Trennung zwischenstofflicher Verbindungen wird wiederum zwischen zwei Fällen unterschieden:

• Handelt es sich um einen rein elastischen Kontakt, so ist die Anzahl gleichartiger Energieanteile gleich der Anzahl der elastischen Kontakte im weicheren Reibkörper.

• Ist der Kontakt elastisch-plastisch oder rein plastisch, so ist mit der plastischen Kontaktanzahl des weicheren Reibkörpers zu rechnen.

Beteiligte Volumina

Die Bestimmung der am Reibungsprozeß beteiligten Volumina ist schwierig. Für die elastische oder plastische Verformung eines repräsentativen Einzelkontaktes kann sie mit der verformten Fläche, der Beanspruchungstiefe und einem Korrekturfaktor (im Bereich von 0,5 bis 1,0 [9]) berechnet werden:

(5.19)

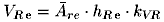
Problematisch ist dabei die Bestimmung der Beanspruchungstiefe. Näherungsweise kann sie für einen elastischen Kontakt als das 1 bis 1,5-fache und für einen plastischen Kontakt als als das ca. 1,1-fache des mittleren Einzelkontaktdurchmessers angenommen werden [8].

Im Falle der Trennung zwischenstofflicher Verbindungen ist das beanspruchte Volumen wesentlich geringer. Daher kann die oben genannte Gleichung für diesen Fall nicht angewendet werden. Stattdessen wird das Verhältnis zwischen Deformations- und Trennvolumen benutzt. Dieses liegt im Bereich von 10² ... 10 ³. Es gilt dann

(5.22)

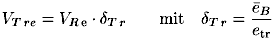
© 1997 Thomas Hooge , André Diercksen, Fachhochschule Hamburg