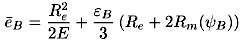
Die Untersuchung der Oberflächen hat das Ziel, die reale Berührungsfläche der Reibkörper zu bestimmen. In diesem Zusammenhang wird die Anzahl der realen Kontaktstellen ermittelt. Diese, sowie die Verformung einer einzelnen Mikroerhebung, hängt von der von außen aufgebrachten Normalkraft bzw. der Pressung ab: je größer die Normalkraft ist, desto mehr Kontaktstellen gibt es und desto größer ist auch die Kontaktfläche eines einzelnen Mikrokontaktes.
Problematisch ist dabei, daß momentan einige Kennwerte der Makrogeometrie zur Reibungsberechnung herangezogen werden, weil die Mikrogeometrie (noch) keine geeigneten Beschreibungsgrößen liefert. Somit werden die durch die Belastung resultierenden Änderungen der Werkstoffoberflächen (z.B. Verfestigungen) nicht berücksichtigt.
Aus dem Spannungs-Dehnungs-Diagramm des einachsigen Zugversuchs können die folgenden Ausgangswerte für die jeweiligen Reibkörper entnommen werden. Für die gebräuchlichen Werkstoffe sind diese Werte aus der Literatur zu entnehmen.
Die mittlere Bruchenergiedichte wird für viele weitere Berechnungen benötigt. Da sie sich ausschließlich aus Werkstoffkennwerten zusammensetzt, wird sie bereits an dieser Stelle berechnet als
| (4.1) |
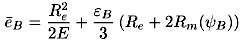
|
Die Oberflächen der beiden Reibkörper sind nicht ideal glatt, sondern weisen Gestaltabweichungen auf [3]. Für die Reibungsberechnung wird die Formabweichung vernachlässigt. Es wird nur nach Welligkeit und Rauhigkeit, wie in Abb.2 zu sehen ist, unterschieden.

Abbildung 2: Profil einer Oberfläche, 1: Welligkeit, 2: Rauhigkeit
Die Oberflächen entstehen durch die bei der Herstellung der Reibkörper angewandten Verfahren. Sie dürfen jedoch nicht in neuem Zustand untersucht (ausgemessen) werden, sondern erst nachdem die Einlaufphase der Reibpaarung abgeschlossen ist. Weiterhin wird angenommen, daß sich das vorhandene Oberflächenprofil der Reibkörper während der gesamten Betriebsdauer (Lebensdauer) stets reproduziert, was auch recht gut mit praktischen Erfahrungen übereinstimmt.
Aus dem Profil der Oberfläche werden folgende für die Reibungsberechnung notwendige Kenngrößen ermittelt:
Die komplexen Oberflächen der Reibkörper müssen zur Berechnung der Reibung in ein mathematisch beschreibbares Modell, das Kontaktmodell, überführt werden. Grundlage für das Kontaktmodell sind die Rauhigkeit und die Härte der Oberflächen.
Die Rauhigkeit der Oberflächen setzt sich aus einer Anzahl von regellosen Mikroerhebungen zusammen. Um diese beschreiben zu können, werden sie im ersten Schritt als Ellipsoide modelliert und anschließend zur Vereinfachung in Kugelabschnitte überführt. Eine andere, kompliziertere Möglichkeit ist es, die Radien der Mikroerhebungen als normalverteilt anzusehen. Auf diese zweite Möglichkeit wird hier aber nicht näher eingegangen.
Die Form der Mikroerhebungen ist somit erfaßt. Die Position und die Höhenlage werden mittels mathematischer Statistik beschrieben und können ohne größere Fehler als Normalverteilt angenommen werden.
Die Aufteilung der Reibungsenergie spielt eine wichtige Rolle und hängt hauptsächlich von der Härte der beteiligten Reibkörper ab. Da die Mikroerhebungen als Kugeln modelliert wurden, bietet sich das Härteprüfverfahren nach Brinell (HB) oder Rockwell B zur Ermittlung der Härten der Reibkörper(oberflächen) an, da der dort verwendete Prüfkörper ebenfalls Kugelform aufweist [4, 5].
Beim Vergleich der Härten der betrachteten Reibkörper wird zwischen zwei Möglichkeiten unterschieden:Die Reibkörperwerkstoffe besitzen in etwa die gleiche Härte. In diesem Fall werden sich bei einem Reibungsprozeß die Mikroerhebungen beider Reibkörper verformen. Dieser Kontakt wird rauh/rauh oder als hart/hart genannt. Zur Modellierung dieses Verhaltens wird das Kontaktmodell Kugel/Kugel benutzt.
Die Reibkörperwerkstoffe weisen sehr unterschiedliche Härten auf. Bei einem Reibungsprozeß werden die Mikroerhebungen des härteren Körpers in den weicheren Körper eindringen. Die Oberflächenmikrogeometrie dieses Körpers spielt so gut wie keine Rolle und wird für die Modellbetrachtung als absolut eben angenommen. Dieser Kontakt wird als rauh/glatt oder als hart/weich bezeichnet. Zur Modellierung wird das Kontaktmodell Kugel/Ebene benutzt.
Bei einem extrem großen Härtesprung ist der Fall eines spanenden Kontakts zu betrachten.
Die Mikroerhebungen der Oberfläche des härteren Reibkörpers werden als Kugelabschnitte betrachtet, die Oberfläche des weicheren Reibkörpers wird als absolut eben angesehen. Das Kontaktmodell ist in der Abbildung 3 skizziert:

Abbildung 3: Kontaktmodell Kugel/Ebene nach [26]
Nähern sich die Reibkörper um den Betrag a an, so kann man aufgrund des Oberflächenprofils die Kontaktanzahl bestimmen. Mit der kritischen Eindringtiefe (siehe Formel 4.9) kann die Gesamtanzahl der Kontakte in elastische und plastische Kontakte aufgeteilt werden.
Dieses Kontaktmodell ist komplizierter als das vorherige, da die Mikroerhebungen beider Oberflächen als Kugelabschnitte aufgefaßt werden. Daher werden einige Annahmen getroffen, um das Problem etwas zu vereinfachen. Es wird vorausgesetzt, daß:
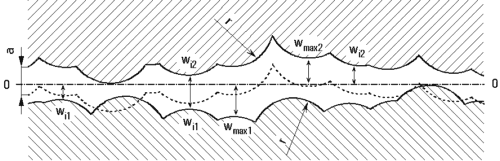
Abbildung 4: Kontaktmodell Kugel/Kugel nach [26]
Der Übergang von rein elastischem Kontakt zu elastisch-plastischem Kontakt tritt bei einer kritischen Annäherung beider Reibpartner auf. Dieser kritischen Annäherung ist die kritische Eindringtiefe zugeordnet mit deren Hilfe sich die Anzahl der elastischen und plastischen Kontakte bestimmen läßt. Es ist
| (4.9) |
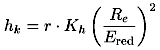
|
Die Kontaktgeometrie liefert für die energetische Betrachtungsweise die folgenden Kennwerte: